Fluid Dynamics Simulation on a Mobile Device

Many physical processes can be simulated using computers. In fact, physics simulations are widely used in a variety of industries: computer games, education, scientific research, engineering and more. Even the flow of water can look very realistic on a computer screen. And considering the growing popularity of mobile devices today, it’s not surprising that we see an increasing demand for hydrodynamic process simulation on mobile devices. Here, I will discuss imitation of paint dispersed on the surface of water, on an iPad.

To make such app look realistic, it is crucial to imitate real physics and what actually happens to the paint as it touches water. In order to do this, we decided to explore some basic hydrodynamics and then make fluid dynamics simulation on an iPad. We are going to use real world formulas that describe water behavior. This process requires large volumes of calculations to be done very quickly. Initially, we tried these calculations on a CPU, but could only produce 5 to 7 frames per second. As we know, in order for eyes to see continuous movement, we need at least 24 frames per second. Clearly, we needed a way to process the data faster. That is why we decided to utilize the GPU in order to try and generate more images per second.

General Purpose Computing on a GPU

Even though the Graphics Processing Unit (GPU) was originally invented to process graphics, it soon became clear that GPUs can be used to carry out many other calculations. For example, GPUs are commonly used in audio and video processing, augmented reality, mathematical calculations, hydrodynamics, cryptography, and many other fields. All these applications can be summed up by the term General Purpose GPU or GPGPU.

As a general rule, the CPU is used to carry out large and complex operations, whereas the GPU is excellent at handling large numbers of simple tasks. When choosing which approach to use, it depends on the task at hand and the amount of data to be processed. If we have a project that involves numerous calculations which are relatively independent of each other, using a GPU is a great idea. In other words, these tasks can be considered parallel.

General Purpose Computing on a GPU is commonly done on PCs, but the real challenge lies when you want to set it up on a mobile device. Just like in the case of PCs, mobile devices have both CPUs and GPUs. However, mobile devices are small in size and have obvious limitations. For example, mobile developers have to keep in mind the battery life. Also, when a computer processes massive amounts of data, we need a good way of cooling the hardware. In case of an iPad, however, we can’t just add more fans and cooling devices, as we are limited by size and weight.

Today, mobile developers lack the proper tools when it comes to using the GPU for things other than graphics. In the case of desktops, we have tools like Nvidia CUDA, AMD FireStream, and Open CL, that are all designed for general calculations on a GPU. For mobile devices, today we only have OpenGL ES, which is designed to handle graphics. That being said, it is possible to do general purpose calculations on OpenGL ES 2.0 system. In our case, we’ll use OpenGL ES 2.0 to process data for a water-painting simulation.

Using OpenGL ES 2.0 for General Purpose Computing

OpenGL makes it possible to produce 2D and 3D graphics using a GPU. OpenGL takes advantage of the so-called ‘graphics pipeline’ to convert primitives (points, lines, etc.) into pixels. The idea behind the pipeline is the following. First, we enter several vertices, thereby loading them into the pipeline. Then, a series of steps is performed with the data entered. As a result, we get an image at the end of the pipeline. In our case, we’re not exactly working with graphics, so we have to do some additional programming to customize OpenGL functionality and carry out physics-related calculations.

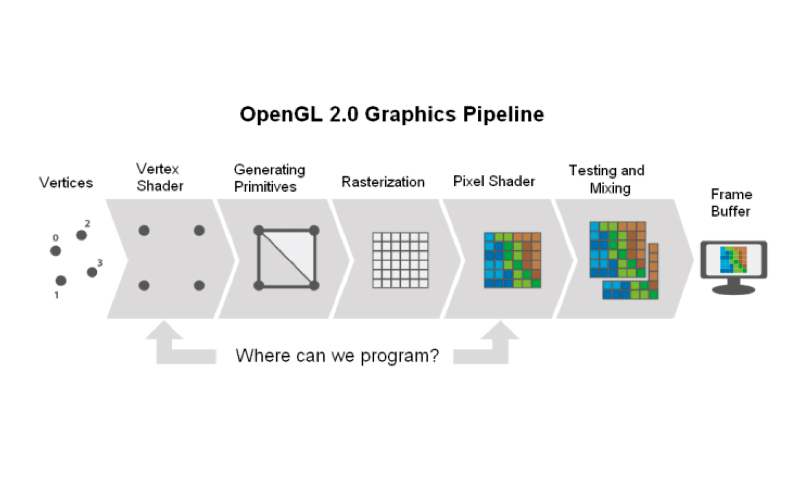
When working with OpenGL, a developer can program only two things: the Vertex Shader and the Pixel Shader. Other steps of the pipeline are carried out automatically. These shaders are essentially two small systems that can be programmed to accomplish a certain task. In our case, all calculations will take place in the Pixel Shader, so we’ll only be programming there. To summarize, the shaders serve as a way to deliver the data to the GPU and ‘tell’ the GPU what calculations to perform.

The Pixel Shader works with four channels: R (red), G (green), B (blue), and A (alpha). In other words, independent calculations can be carried out in each one of these channels simultaneously. Furthermore, the shaders of OpenGL can be programmed using a special programming language called OpenGL Shading Language (GLSL). It is a shading language that is based on C-programming language syntax. It is very similar to ANSI C language, with some additional elements that allow working with vectors and matrices.

Simulation of Fluid Dynamics

There are numerous approaches to simulating the movement of water on a computer screen. One of them is the Lattice-Boltzman Method, which can be applied to this situation. This method looks at liquid as if it were a collection of fictive particles. At the core of this method is a uniform rectangular grid or lattice, where every cell of the grid has several parameters. The parameters include density of the particles, vector speed of the particles, and 9-speed channels. To illustrate this concept, let’s say we have a puddle of water and place an imaginary grid over it. Now, water particles in every cell can be stationary, or they can be moving in a certain direction. If we’re dealing only with the surface of water, we only need to think two-dimensionally. However, keep in mind that this method is often used for 3D simulations, in which case the number of channels would be significantly larger.

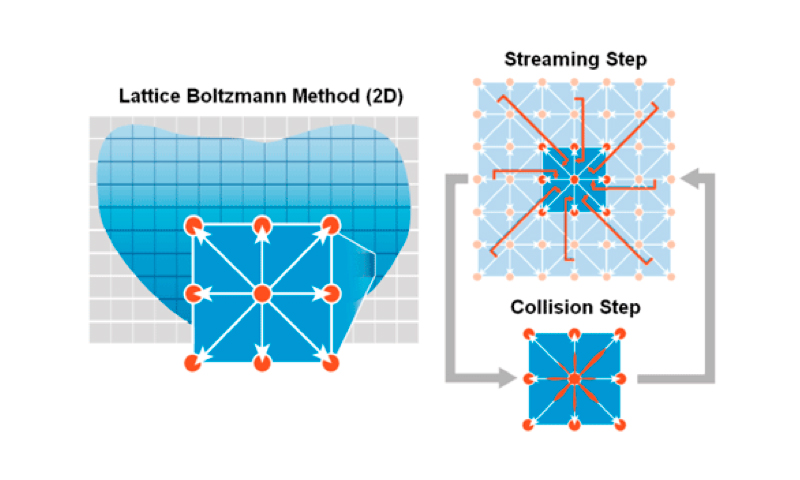
Every part of the liquid is represented by a small cell of our grid. Whenever we have some kind of movement in the water, we use real-world hydrodynamics formulas to predict the outcome. Any change in the grid happens in two steps: the collision step and the streaming step. In the collision step, all calculation happen within the cell, so these calculations are independent of anything that occurs elsewhere. Such calculations are great candidates for parallel processing, so they can be done on a GPU. The streaming step has to do with looking at what happens in nearby cells and applying it to the cell of interest.

In the beginning, we have a disruption-free liquid surface, all particles are stationary. The particles are uniformly dispersed all across the surface, so we assign 1 for our density parameter. Recall that we have four channels in the pixel shader, RGBA. The density parameter would be assigned to the R channel, x-speed to the G channel, and y-speed to the B channel. The A channel is not used.

Now, imagine someone is touching or moving the finger across the iPad screen. This supplies values for x and y coordinates (depending on which cell is being stimulated) as well as x and y speed (if you’re moving your finger across the screen). So, we plug these values into a formula for collision step and calculate density in each speech channel. Next, we need to copy the values of corresponding speed channels from neighboring cells. If there’s some activity in neighboring cells, it will spread to this cell. The concept is very similar to the way particles float on the surface of a liquid.

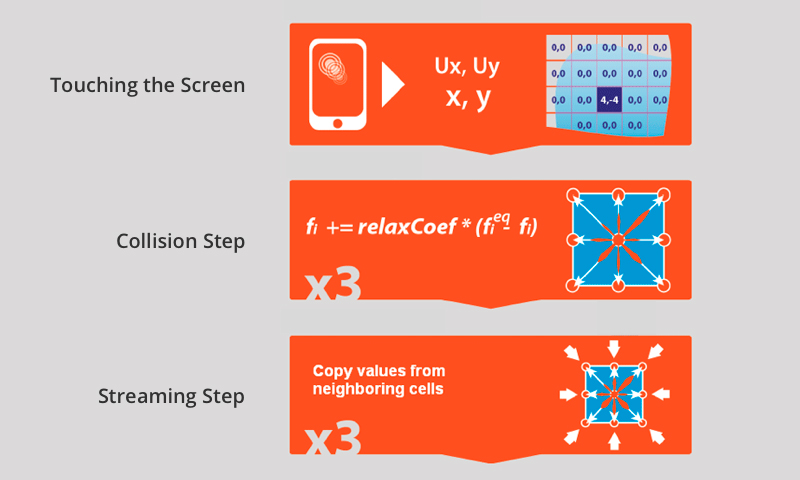
To visualize this movement on the screen we can record the value for the vector of combined x and y speeds into the red channel. As a result, we will see red color being dispersed on the screen, just like red paint would be dispersed in a container of water.

While the Lattice Boltzmann method proved to be a good fit for simulating paint on the surface of water, it cannot be applied to many other fluid dynamics simulations. The experience we gained while working with Lattice Boltzmann method helped us address other similar projects. For example, we came up with another computational method based on the Navier-Stokes equations when developing AquaReal, an iPad app that imitated watercolor painting. In order to imitate color blending realistically, we relied on Kubelka-Munk compositing model algorithm, though it had to be modified significantly to solve all the challenges.

iPad users can view the results of our research by taking a look at the applications we’ve developed: AquaReal watercolor painting app, which I mention above, as well as WaterHockey game. Both applications are available for free at the App Store.

Simulation of Multi-Component, Multi-Phase Fluids Using LBM

Simulating and modeling a two-component viscous fluid is based on a fairly common approach, which was first proposed by Xiaowen Shan and Hudong Chen in 1994. The main idea of their approach is to introduce an additional force that acts on fluid particles. In our case, it provides additional components which modify the speed in each lattice site. These components are calculated as a function of liquid density in the neighboring sites, multiplied by a constant value (potential for interaction), which defines the amplitude of interaction forces. At the same time, we can still take advantage of the fact that it is relatively easy to set-up parallel processing and carry out calculations on a GPU.

Outcome

The resulting simulation of paint dispersion in water looks very realistic. To test if this approach works, we tried it on an iPad 2 and set-up our grid to be 256×256 pixels. In the end, we were able to produce 38 frames per second, as opposed to the original 7 frames that were produced by the CPU. This illustrates the benefits of using a GPU to carry out parallel tasks.

No doubt, the method described above could have been simplified if OpenCL framework was supported by our mobile device. After all, OpenCL framework is specifically designed for general purpose calculation on a GPU. We hope that OpenCL will someday become available on iOS devices as it would simplify working with the GPU. But for the time being, OpenCL isn’t an option so we have to rely on OpenGL to carry out general purpose computing on GPU of a mobile device.